【GESP】C++二级练习 luogu-b3686, [语言月赛202212] 洛谷三角洲

GESP二级练习，数学函数，难度★✮☆☆☆。

luogu-B3686 [语言月赛202212] 洛谷三角洲

题目要求

题目描述

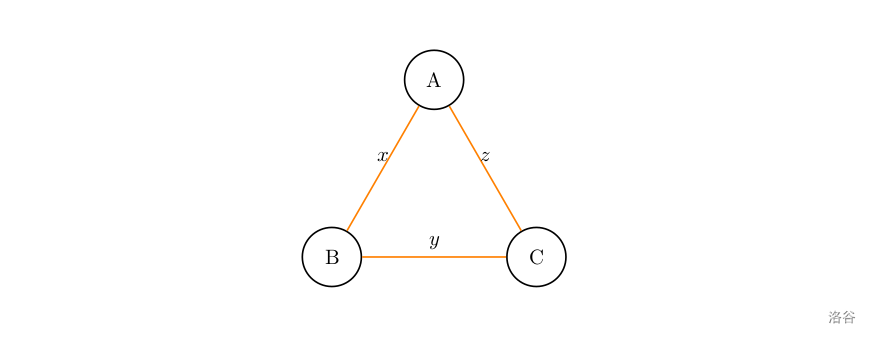
在平行的洛谷世界，有 A，B，C 三座城市，它们构成了洛谷三角洲。

两两城市之间各有一条双向道路。也就是说，一共有三条道路，A 市与 B 市之间有一条道路，A 市与 C 市之间有一条道路，B 市与 C 市之间有一条道路。

由于每条道路的拥堵程度不同，因此通过一条路需要的时间也不同。对于每一条路，双向的拥挤程度相同（即经过 A 市与 B 市之间的一条道路，由 A 市到 B 市和由 B 市到 A 市所需的时间相同）。

通过 A 市与 B 市之间的道路需要 $x$ 分钟，通过 B 市与 C 市之间的道路需要 $y$ 分钟，通过 C 市与 A 市之间的道路需要 $z$ 分钟。

由于业务需要，洛谷站长需要在三个市之间频繁往返。如果能够知道任意两个市之间通行的最短时间，那么他能够极大地提高工作效率。

所以他现在想知道：从 A 市到 B 市，从 B 市到 C 市，从 A 市到 C 市分别至少需要多少时间（单位：分钟）。但是他认为这个问题太难了，所以他把这个问题交给了聪明的你。

输入格式

输入共一行，共三个整数，分别表示 $x,y,z$。

输出格式

输出共三行：
第一行为从 A 市到 B 市至少需要的时间。
第二行为从 B 市到 C 市至少需要的时间。
第三行为从 A 市到 C 市至少需要的时间。

样例输入 #1

1 2 5

样例输出 #1

1
2
3

样例输入 #2

3 3 3

样例输出 #2

3
3
3

提示

样例 1 解释

从 A 市到 B 市需要 $1$ 分钟，从 B 市到 C 市需要 $2$ 分钟。
从 A 市到 C 市可以先从 A 市到 B 市，再从 B 市到 C 市，这样只需要花费 $1+2=3$ 分钟。

数据规模与约定

• 对于 $20\%$ 的数据，满足 $x=y=z$；
• 对于另外 $20\%$ 的数据，满足 $x+y\ge z$，$x+z\ge y$，$y+z\ge x$；
• 对于 $100\%$ 的数据，满足 $1 \leq x,y,z\le 10^9$。

---

题目分析

本题的关键是理解从 A 市到 C 市的最短时间是通过 A 市到 B 市再到 C 市的时间和直接从 A 市到 C 市的时间的最小值。同理，从 B 市到 C 市的最短时间是通过 B 市到 A 市再到 C 市的时间和直接从 B 市到 C 市的时间的最小值。从 A 市到 B 市的最短时间是直接从 A 市到 B 市的时间。

因此，我们可以通过比较直接的时间和通过中转的时间来找到最短的时间。然后输出这些最短时间。

在代码实现中，我们可以使用min函数来比较直接的时间和通过中转的时间，并输出最小的时间。

示例代码

#include <cmath>
#include <iostream>

using namespace std;
int main() {
    int x, y, z; // 定义变量x, y, z
    cin >> x >> y >> z; // 从输入流中读取x, y, z的值
    cout << min(x, y + z) << endl; // 输出x和y+z的最小值
    cout << min(y, x + z) << endl; // 输出y和x+z的最小值
    cout << min(z, x + y) << endl; // 输出z和x+y的最小值
    return 0;
}

---

所有代码已上传至Github：https://github.com/lihongzheshuai/yummy-code

GESP各级别考纲要点、知识拓展和练习题目清单详见C++学习项目主页

“luogu-”系列题目已加入洛谷Java、C++初学团队，作业清单，可在线评测，团队名额有限，欢迎加入。

“bcqm-”系列题目可在编程启蒙题库进行在线评测。